An asteroidal companion to the Earth
appeared in Nature, 1997, vol 387, 685-686.
Paul Wiegert and Kimmo Innanen
Department of Physics and Astronomy
York University
4700 Keele Street
North York, Ontario
M3J 1P3 Canada
Seppo Mikkola
Tuorla Observatory
University of Turku
21500 Piikkiö Finland
Near-Earth asteroids (or NEAs) are our closest neighbours in the Solar
System-- some of these objects have been known to pass closer to the
Earth than the Moon (1). These objects, which range in size from
40 km to a few metres, are important to our understanding of past
and present Earth impact rates, and are likely to prove useful as
bases and/or mineral sources as humans move into near-Earth
space. Here we report that the near-Earth asteroid 3753 (1986 TO) is
in an unusual horseshoe-type orbit about that of the Earth. Horseshoe
orbits, so named because of their shape in a reference frame which
corotates with their accompanying planet, are a well-known feature of
the three-body problem (2). However, only one instance of this type of
interaction has been observed in nature, involving the Saturnian
satellites Janus and Epimetheus (3) , and this system's behaviour is
much less intricate than that of 3753. This asteroid is unique: it is
an example of a rare type of dynamical relationship, and although it
is not a satellite of our planet per se, it is, apart from the
Moon, the only known natural companion of the Earth.
Figure 1 presents a view of the inner Solar System projected onto
the ecliptic plane in a frame which corotates with the Earth; in this
frame, the Earth is stationary. The path of asteroid 3753 over a
little more than one year indicated by the line with arrowheads. The
path has roughly the shape of a kidney bean, owing simply to the
eccentricity of the asteroid's orbit. As the asteroid's orbital
period is slightly shorter than that of the Earth, its orbit does not
close on itself but rather advances slightly each year; the asteroid
thus spirals forward along the orbit of the Earth.
This behaviour is not unusual in itself: what differentiates 3753 from
other NEAs is its behaviour as it approaches the Earth. A typical
close encounter between the Earth and an NEA results in a large change
in the asteroid's orbit, with collision being a distinct, if remote,
possibility. However, the dynamical relationship between the Earth
and 3753 is such that a much milder interaction occurs. As the
asteroid approaches, our planet's gravitational pull acts to increase
the asteroid's period to a value slightly greater than one year. As a
result, the asteroid begins to fall behind, and hence to move away
from, our planet. A possible collision with the Earth is avoided; the
closest approach during this leg is indicated by the heavy line A in
Figure 1.
When the asteroid eventually approaches the Earth from the other
direction, the Earth's gravity will again influence the asteroid's
orbit. In this case, however, the asteroid's period decreases to its
previous value slightly below that of the Earth; thus the asteroid is
again effectively repelled and begins moving away from the Earth. At
closest approach on this leg, the edge b of the kidney bean
coincides with the heavy line labeled B in Figure 1. The cycle of
reversals then goes on to repeat itself. The previous two reversals
occurred in approximately AD 1515 and 1900; the next two will occur in
2285 and 2680. The variation in semi-major axis of 3753 over the next
two thousand years is presented in Figure 2. The reversals correspond
to transitions across the semi-major axis of the Earth (1 AU).
It should be noted that these reversals occur when edge a (not
b) approaches the Earth. Owing to the asteroid's orientation
and inclination, edge b is not near the Earth's orbit, despite
its appearance when projected onto the ecliptic plane. Figure 3
presents a view of the inner Solar System from an ecliptic-on
perspective, and the asteroid's high inclination (20 degrees ) is
evident. The orientation of the asteroid's orbit allows edge b
to overlap the position of the Earth with no danger of collision. The
complete orbit of 3753 is thus an ``overlapping horseshoe'' (the outer
envelope of which is indicated by the heavy line in Figure 1), a kind
which has never been observed before, even in theoretical studies.
The asteroid's significant inclination and eccentricity (approx. 0.5)
has evidently caused it to escape more intensive scrutiny since its
discovery, as they serve effectively to obscure the nature of its
trajectory.
The asteroid's orbit is chaotic, with an e-folding time of 150
years, but it remains a near-Earth object in our simulations for time
scales of a million years. However, not all of this time is spent as a
horseshoe: the asteroid switches between its current orbit and a
non-horseshoe orbit with semimajor axis around 1.1 AU on time scales
of a few hundred thousand years.
Asteroid 3753 passes from inside to outside the Earth's orbit, but its
minimum yearly approach distance is usually quite large. During the
closest approaches, which happen only every 385 years, the asteroid
passes within 0.1 AU (roughly 40 times the Earth-Moon distance)
of our planet, the last such approach having occurred about 100 years
ago. Over the next year, the closest approach will be only to within
0.31 AU. The relative proximity of 3753 to the Earth during
recent times presumably aided in its discovery by D. Waldron on Oct
10, 1986 at Siding Spring, Australia (4,5) . Asteroid 3753 has an
absolute visual magnitude of 15.1 (6), brighter than typical of
NEAs, and from which one can estimate a diameter of 5 km
(7,8).
Asteroid 3753 crosses the orbits of Venus and Mars as well as the
Earth's. Though its orbit does not currently intersect that of any
planets, the asteroid's argument of perihelion precesses at a rate of
roughly +0.6 degrees per century. As a result, its orbit will
intersect that of the Earth in 2750 years, and (if it survives this
crossing) that of Venus in about 8000 years. Similarly, the asteroid's
orbit intersected Mars' roughly 2500 years ago. These results suggest
that the asteroid's current horseshoe orbit may not be stable for
arbitrarily long times, unless there is some dynamical ``safety
mechanism'' which preserves it against close planetary encounters. At
this point, the existence of such a safety mechanism seems unlikely,
and yet the very low a priori probability of an object being
injected into such an orbit makes a recent origin seem equally
unlikely. As for the prediction of the asteroid's future, problematic
owing to its short e-folding time, a collision with the Earth
seems very improbable. A strong gravitational interaction with Venus
in 8000 years seems quite likely, though the possibility of a
collision with that planet at that time remains remote.
Methods: The numerical simulations of asteroid 3753 presented here
were performed with the Wisdom-Holman (9) integrator, in a model Solar
System which included all the planets except Pluto. It should be noted
however that the Earth-Moon barycentre was used for the Earth, an
approximation which is valid because the Earth-asteroid distance is
always much larger than the Earth-Moon distance. The heliocentric
orbital elements of 3753 used were: semimajor axis a =
0.99778030 AU, eccentricity e=0.51478431, inclination
=19.812285 degrees, longitude of the ascending node=126.373212 degrees
, argument of perihelion = 43.640637 degrees , and mean anomaly =
40.048932 degrees , these elements being calculated for epoch JD
2450500.5 and the equinox of J2000.0 (6).
References:
- (1) Scotti, J. V., Rabinowitz, P. L., and Marsden, B. G., Near
miss of the earth by a small asteroid, Nature, 354, 287-289
(1991).
- (2) Szebehely, V., Theory of Orbits, Academic Press:
New York (1967).
- (3) Synnott, S. P., Peters, C. F., Smith, B. A., and Morabito,
L. A., Orbits of the small satellites of Saturn, Science, 212,
191-192 (1981).
- (4) Minor Planet Circular 11312, Minor Planet Center,
Smithsonian Astrophysical Observatory, Cambridge (1986).
- (5) IAU Circulars 4262 and 4266, Central Bureau for Astronomical
Telegrams, Smithsonian Astrophysical Observatory, Cambridge (1986).
- (6) Bowell, E., The Asteroid Orbital Elements Database,
an electronic publication available at
ftp://ftp.lowell.edu/pub/elgb/astorb.html (1997).
- (7) Bowell, E., Hapke, B., Domingue, D., Lumme, K., Peltoniemi,
J. and Harris, A. W., Application of photometric models to
asteroids, in Asteroids II, Binzel, R. P. et al. (eds.), The
University of Arizona Press, Tucson, pp. 524-556 (1989).
- (8) Rabinowitz, D. L., The size distribution of
earth-approaching asteroids, Astrophys. J., 407, 412-427 (1993).
- (9) Wisdom, J. and Holman, M., Symplectic maps for the n-body problem, Astron. J, 102, 2022-2029 (1991).
Acknowledgements: We would like to thank Matt Holman for the
use of his numerical code, and the referees for their helpful
comments. This work has been supported in part by the National
Sciences and Engineering Research Council of Canada. Correspondence
and requests for material to P.A.W., (wiegert@yorku.ca).
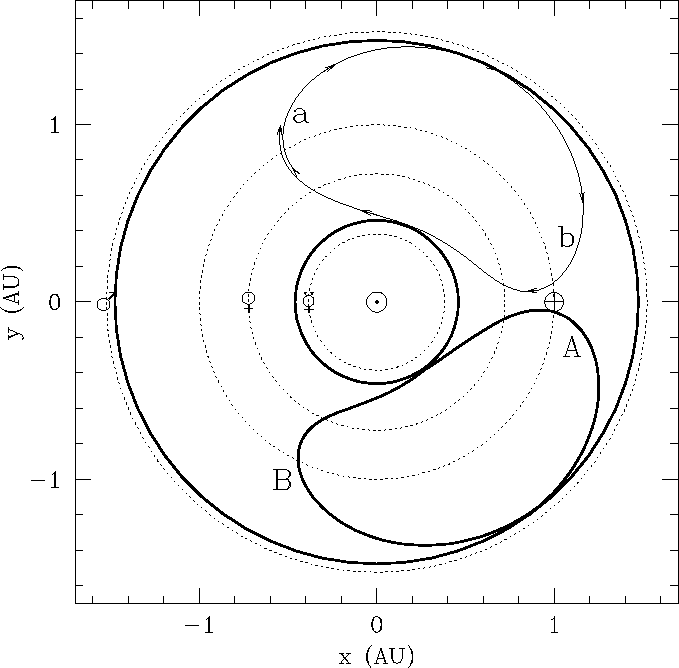
Figure 1: A
view of the inner Solar System projected onto the ecliptic plane in a
frame which corotates with the Earth; in this frame, the Earth is
stationary and is located at the crossed circle. The average distances
of the planets Mercury, Venus, Earth and Mars from the Sun are
indicated by the dotted circles. The path of asteroid 3753 over
slightly more than a year, beginning approximately in AD 2000, is
shown by the line with arrowheads. The extremes of the horseshoe are
indicated by the heavy lines. One extreme occurs when a
coincides with A, the other when b coincides with
B.
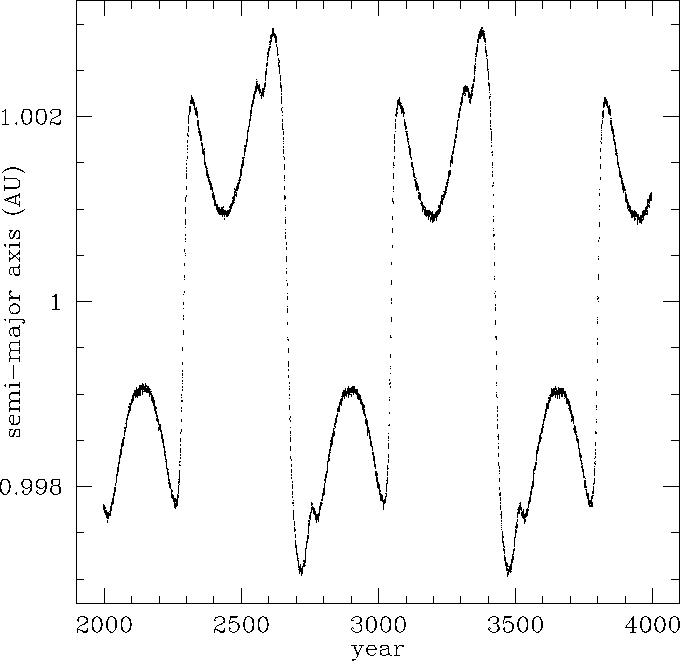
Figure: The
heliocentric semimajor axis a of asteroid 3753 (1986 TO) over
the next two thousand years, in astronomical units (AU). Transitions
from a >1 AU to a < 1 AU or vice-versa correspond to reversals of the
asteroid's direction within the horseshoe.
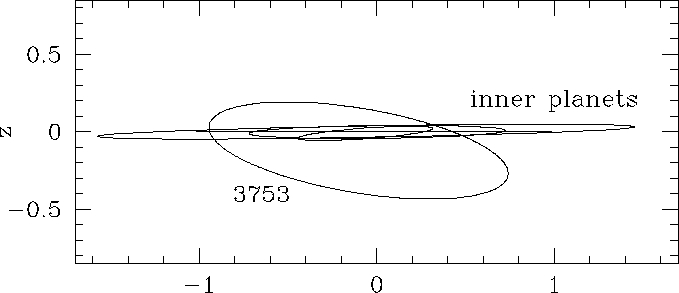
Figure 3: The orbits of the inner planets Mercury, Venus, Earth and
Mars, along with that of asteroid 3753 when seen from the direction of
the vernal equinox. The Sun is at the origin, and the units are
astronomical units.


