

Nuclear sizes and ground states
- The binding energy of a nucleus is a very important
characteristic for stability, because of the various ways in which a
nucleon can change to another or escape altogether. If the binding
energy of the initial state is less than the total of the final
states, decay (conversion of one system into a different one) is
possible.
- The binding energy
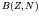 may be measured directly by
disassembling a nucleus, but it is often convenient to measure it by
measuring the mass of the nucleus, or of the (usually neutral) atom:
may be measured directly by
disassembling a nucleus, but it is often convenient to measure it by
measuring the mass of the nucleus, or of the (usually neutral) atom:
where 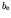 is the total electronic binding energy, ranging from
13.6 eV for H to several hundred keV for uranium.
is the total electronic binding energy, ranging from
13.6 eV for H to several hundred keV for uranium.
- If we look at binding energy of light nuclei, we find (1) an
average binding energy per nucleon that rises rapidly from about 1
MeV per particle for the deuteron to near 8 MeV per particle, (2)
relatively high binding energy per nucleon for ``even-even'' nuclei
such as
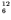 C, and (3) rather small binding energy of the
``last'' nucleon for nuclei with one particle above even-even, rising
to considerably larger values for the last nucleon as the next
even-even nucleus is approached. There is clearly some important
binding energy associated with neutron-neutron and proton-proton
pairing.
C, and (3) rather small binding energy of the
``last'' nucleon for nuclei with one particle above even-even, rising
to considerably larger values for the last nucleon as the next
even-even nucleus is approached. There is clearly some important
binding energy associated with neutron-neutron and proton-proton
pairing.
- The binding energy per nucleon of
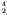 He is so high that it
is energetically advantageous for
He is so high that it
is energetically advantageous for 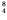 Be to break up into two He
nuclei, in spite of its even-even nature. This is an example of the
ease with which He nuclei (alpha particles) can be formed.
Be to break up into two He
nuclei, in spite of its even-even nature. This is an example of the
ease with which He nuclei (alpha particles) can be formed.
- The total binding energy of nuclei of various
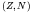 combinations may be fitted by a reasonably accurate approximate
formula involving only a few parameters. One form of this equation is
combinations may be fitted by a reasonably accurate approximate
formula involving only a few parameters. One form of this equation is
where the parameters are determined by fitting the ensemble of
measured binding energies. The best fits for this form are
and  is 0 for even-odd nuclei,
is 0 for even-odd nuclei, 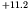 MeV for odd-odd nuclei,
and
MeV for odd-odd nuclei,
and 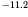 MeV for even-even nuclei.
MeV for even-even nuclei.
- In this formula, the various terms all have physical
interpretations. The first term represents the mean energy per nucleon,
approximately constant over the periodic table because the strong
force, with its very short range, only binds nearest neighbors
together. The second term is a surface term which reflects the
decrease in binding energy due to nucleons on the surface where they
are bound to fewer other nucleons than interior nucleons are. The
fourth term describes the repulsive influence of the positive charges
of the protons, and is approximately equal to the total energy of
repulsion of a uniform sphere of total charge
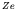 within radius
within radius 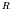 .
.
- The third term reflects the effect of the exclusion principle,
and is the simplest form that forces
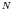 to be approximately equal to
to be approximately equal to
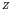 . The reason for this ``symmetry'' term is that if we think of the
energy levels within the nucleus as single-particle states like atomic
orbitals, we can put two protons (spin up and spin down) into each
level, and two neutrons. If we replace one of the protons by a
neutron, the new neutron cannot go in the level of the former proton,
but must go to the next level up. Thus it must have a higher energy
than the proton it replaces. This effect favours
. The reason for this ``symmetry'' term is that if we think of the
energy levels within the nucleus as single-particle states like atomic
orbitals, we can put two protons (spin up and spin down) into each
level, and two neutrons. If we replace one of the protons by a
neutron, the new neutron cannot go in the level of the former proton,
but must go to the next level up. Thus it must have a higher energy
than the proton it replaces. This effect favours 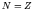 . The
. The 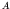 in
the denominator makes this term proportional to the total number of
nucleons for a fixed ratio
in
the denominator makes this term proportional to the total number of
nucleons for a fixed ratio 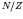 .
.
- Finally, the term with
 describes the strong tendency of
identical nucleons to prefer to occur in pairs. Thus even-even
nuclei are on average considerably more strongly bound than odd-odd
nuclei even if the last nuclear orbital is unfilled. The
describes the strong tendency of
identical nucleons to prefer to occur in pairs. Thus even-even
nuclei are on average considerably more strongly bound than odd-odd
nuclei even if the last nuclear orbital is unfilled. The 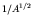 dependence is empirical; it reflects the fact that the pairing energy
contribution is smaller in heavy nuclei than light ones.
dependence is empirical; it reflects the fact that the pairing energy
contribution is smaller in heavy nuclei than light ones.
- Many nuclei are observed to be unstable: they spontaneously
change into other nuclei by emission of one or more particles. The two
common kinds of decay of naturally occurring nuclei are
- beta-decay: emission of an electron or
positron, or absorption of an atomic electron, with conversion of a
proton into a neutron or vice versa. An example is
- alpha-decay: emission of a
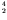 He nucleus (an
alpha-particle). An example is
He nucleus (an
alpha-particle). An example is
- Such decays occur when the nucleus in question can go to a state
of lower energy by the decay, and enough energy is available from the
transition to supply what is needed for the decay (e.g to create an
electron and a neutrino).
- Consider beta-decay. In this decay, no nucleons are
lost by the nucleus, so
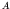 stays constant, while
stays constant, while
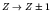 and
and
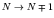 .
.
- Although simple, the binding energy formula is accurate enough to
predict correctly - in almost all cases - which nuclei are stable
against beta-decay. Using our simple form, and substituting
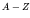 for
for
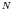 , the mass of a particular atom is
, the mass of a particular atom is
This expression is a parabola in 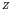 , opening upward.
, opening upward.
- For odd
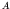 ,
, 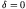 both before and after a beta-decay,
since either
both before and after a beta-decay,
since either 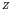 or
or 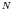 is odd both before and after decay. In this
case, we may find the most stable
is odd both before and after decay. In this
case, we may find the most stable 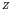 value for a given
value for a given 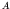 by finding
the minimum of the expression above:
by finding
the minimum of the expression above:
The actual 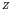 of lowest energy,
of lowest energy, 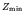 , is the integer value
nearest the computed
, is the integer value
nearest the computed 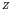 .
Since
.
Since
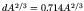 MeV is larger than
MeV is larger than
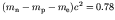 MeV for
MeV for 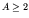 we see at once
that
we see at once
that
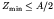 and
and
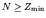 .
.
- Since the
 is (nearly) massless, beta-decay is possible if
is (nearly) massless, beta-decay is possible if
Adding 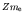 to each side, this may be expressed using atomic
masses as
to each side, this may be expressed using atomic
masses as
- If
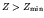 , decay can occur by positron emission
if
, decay can occur by positron emission
if
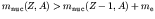 or
or
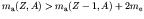 .
.
- In an atom, another process that competes with positron emission
is electron capture or K-capture. The nucleus absorbs an
electron from its cloud (usually from the K shell), converting a
proton to a neutron and emitting a neutrino. K-capture is possible if
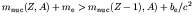 ,
or
,
or
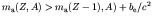 .
The binding energy
.
The binding energy 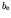 that must be supplied by the capture
may be as much as 100 keV, but this is less than the two electron
masses required by positron emission, so K-capture may be possible
when
that must be supplied by the capture
may be as much as 100 keV, but this is less than the two electron
masses required by positron emission, so K-capture may be possible
when 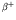 -emission is not.
-emission is not.
- We thus expect that there will be only one stable isobar of a
given odd
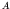 . This is in fact the case.
. This is in fact the case.
- Nuclei with even
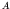 either have both
either have both 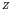 and
and 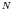 even, or both
odd. Beta-decays will change an odd-odd nucleus to an even-even one,
and vice versa. For these two situations, the binding energy term in
even, or both
odd. Beta-decays will change an odd-odd nucleus to an even-even one,
and vice versa. For these two situations, the binding energy term in
 has opposite signs, so there will be two mass parabolas
for fixed
has opposite signs, so there will be two mass parabolas
for fixed 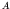 as a function of
as a function of 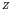 , one
, one
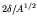 above the
other. Again
above the
other. Again 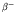 or
or 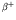 decays are possible from higher to
lower mass atoms, but now we generally expect to find one, two, or
even three minimum
decays are possible from higher to
lower mass atoms, but now we generally expect to find one, two, or
even three minimum 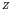 values on the lower parabola, separated by
higher odd-odd nuclei, and no minimum
values on the lower parabola, separated by
higher odd-odd nuclei, and no minimum 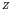 values on the upper
parabola. This is observed to be true with two exceptions,
values on the upper
parabola. This is observed to be true with two exceptions,
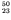 V and
V and 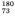 Ta.
Ta.
- An example (from third-year lab) of successive decays for even
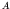 leading to stability is
leading to stability is
followed by
The Zr is stable. Note that the second decay releases more energy than the
first.
- To summarize, for given
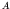 (isobars) we expect to find only
one stable
(isobars) we expect to find only
one stable 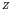 if
if 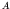 is odd, and one, two or three if
is odd, and one, two or three if 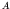 is even.
Furthermore, the trend of beta-stable nuclei in a diagram plotting
is even.
Furthermore, the trend of beta-stable nuclei in a diagram plotting 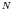 against
against 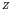 (a ``Chart of the Nuclides'') is accurately reproduced.
(a ``Chart of the Nuclides'') is accurately reproduced.
- The binding energy per nucleon,
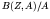 , may be plotted as a
function of
, may be plotted as a
function of 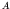 for the stable nuclei of
for the stable nuclei of 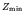 . If the plot is
restricted to odd-
. If the plot is
restricted to odd-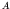 nuclei, the scatter is quite small.
nuclei, the scatter is quite small. 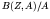 rises from just over 1 MeV per nucleon in the deuteron to about 8.7
MeV per nucleon for the elements around iron (
rises from just over 1 MeV per nucleon in the deuteron to about 8.7
MeV per nucleon for the elements around iron (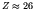 ,
, 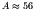 ). From there it declines slowly to below 7.8 MeV per
nucleon beyond
). From there it declines slowly to below 7.8 MeV per
nucleon beyond 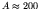 .
.
- The positive binding energy is entirely contributed by
the strong nuclear interaction, diminished somewhat by surface effects
and by the effects of a difference between
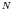 and
and 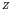 . However, the
effect that actually causes
. However, the
effect that actually causes 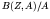 to decline above
to decline above 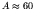 is the increasing Coulomb repulsion among the nucleons. Because the
strong force acts only between nearest neighbors, it increases only as
is the increasing Coulomb repulsion among the nucleons. Because the
strong force acts only between nearest neighbors, it increases only as
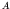 (not
(not 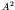 ), while the electrostatic repulsion increases about as
), while the electrostatic repulsion increases about as
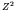 , and thus becomes more important as
, and thus becomes more important as 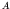 and
and 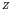 increase.
increase.
- The fact that the binding energy per nucleon
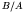 decreases
beyond
decreases
beyond 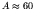 means that decays in which the nucleus breaks
into two smaller pieces may be able to release energy, and thus become
possible.
means that decays in which the nucleus breaks
into two smaller pieces may be able to release energy, and thus become
possible.
- Of such decays, alpha-instability is the most common,
because the decay leads to ejection of a tightly bound
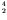 He nucleus, making the 28.3 MeV binding energy of this
nucleus available. All nuclei of
He nucleus, making the 28.3 MeV binding energy of this
nucleus available. All nuclei of 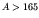 can release energy by
ejecting an alpha-particle, but (as we will see later) the rate is
often so slow as to be insignificant even over the age of the
universe.
can release energy by
ejecting an alpha-particle, but (as we will see later) the rate is
often so slow as to be insignificant even over the age of the
universe.
- Another possible decay mode is fission, in which a heavy
nucleus breaks into two smaller, roughly equal fragments, each with
higher
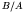 than the original nucleus.
than the original nucleus.
The semi-empirical mass formula describes the stability
behaviour of nuclei quite well. However, although we presented
arguments for the form of each term, we fixed the coefficients purely
empirically. We now look at simple quantum models of the nucleus and
see what kinds of quantitative conclusions may be drawn about nuclear
structure from such models.
Consider what kind of potential we need to write down the
Hamiltonian of the system. We do not know the details of the nuclear
interaction. Let's suppose, as in many-electron atoms, that each
individual nucleon moves in a spherically symmetric potential created
by the other nucleons. This potential, because of electrostatic
repulsion, will be somewhat different for protons than for
neutrons. Since there is no attracting centre to the system (analogous
to the atomic nucleus in a many-electron atom) we expect that the
nuclear potential may be roughly describable as a strong force
preventing each nucleon from leaving the nucleus, but the apparently
uniform density within the nucleus suggests that there is no strong
tendency for nucleons to be in any one part of the nucleus rather than
another.
This suggests that we could roughly describe the nuclear
potential as a simple rectangular potential well with a flat
floor. For neutrons, the well would have a depth and radius, and be
zero outside the nucleus. For protons the well would be raised by
electrostatic repulsion, and outside the nucleus would fall off to 0
at infinity from a substantial positive value. To really simplify
matters, however, let's start by taking the wells to be infinitely
deep.
Now we estimate the parameters of these two wells. Note that
nucleons are fermions, and thus obey the exclusion principle. Thus we
expect that - roughly - they will fill up the lowest states in the
nuclear potential, up to some upper level 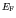 . Each state will
have one neutron and one proton of each spin direction. To estimate
how many states are available, we need a very useful result
concerning the density of states that we have met before.
Consider the solution of the Schroedinger equation in a large
box with sides at
. Each state will
have one neutron and one proton of each spin direction. To estimate
how many states are available, we need a very useful result
concerning the density of states that we have met before.
Consider the solution of the Schroedinger equation in a large
box with sides at 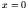 and
and 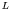 ,
, 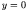 and
and 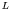 ,
, 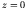 and
and
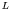 . The potential is zero inside the box, and infinite outside. In the
box,
. The potential is zero inside the box, and infinite outside. In the
box,
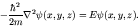
We can clearly separate variables. Solutions satisfying 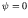 on
the boundaries of the box are
on
the boundaries of the box are
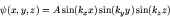
where the wave numbers must satisfy
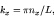
etc, with 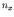 ,
, 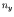 and
and 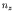 positive integers, and (from the
Schroedinger equation)
positive integers, and (from the
Schroedinger equation)
The states with energies less than some particular energy
(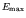 , say) are all the values of
, say) are all the values of 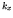 , etc for which
, etc for which
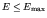 . Now the allowed states are uniformly spaced
in k-space because of the relationship between
. Now the allowed states are uniformly spaced
in k-space because of the relationship between 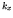 and
and 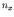 ,
etc, and in a small volume of k-space of
,
etc, and in a small volume of k-space of
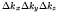 there are
there are
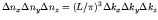 states. Thus the total number of of
allowed states in the box of energy up to
states. Thus the total number of of
allowed states in the box of energy up to 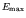 is
is

where the factor 2 comes from two spin states, the factor 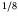 is the
volume fraction in the quadrant having all positive values of
is the
volume fraction in the quadrant having all positive values of 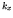 ,
etc (only positive values lead to distinguishable states), and
,
etc (only positive values lead to distinguishable states), and 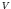 is
the total volume of the box.
Now apply this result to our nucleus. We have noted that
the number densities of neutrons and protons are nearly equal and are
constant independent of
is
the total volume of the box.
Now apply this result to our nucleus. We have noted that
the number densities of neutrons and protons are nearly equal and are
constant independent of 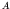 , each at about 0.085 nucleons
fm
, each at about 0.085 nucleons
fm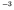 . Equating this value to the
. Equating this value to the
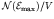 above,
we deduce that the neutron (and proton) energy states in the nucleus
will be filled up to a maximum (Fermi) energy
above,
we deduce that the neutron (and proton) energy states in the nucleus
will be filled up to a maximum (Fermi) energy 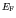 of about 38
MeV above the bottom of the nuclear potential well.
The approximation above assumes an infinitely deep well, but
does not change very much for a potential well of finite depth. We can
estimate the total depth of the well by recalling that the
typical binding energy per nucleon is about 8 MeV, so the total depth
of the nuclear potential well is roughly 46 MeV.
Using this simple model of single-nucleon states in the
nuclear potential well, we can easily see what happens in nuclear
beta-decay, when there is (say) an excess of protons over neutrons in
the nucleus: a proton can release enough energy by becoming a
neutron and dropping into a lower unoccupied neutron state to pay for
the energy required to create the positron and neutrino.
of about 38
MeV above the bottom of the nuclear potential well.
The approximation above assumes an infinitely deep well, but
does not change very much for a potential well of finite depth. We can
estimate the total depth of the well by recalling that the
typical binding energy per nucleon is about 8 MeV, so the total depth
of the nuclear potential well is roughly 46 MeV.
Using this simple model of single-nucleon states in the
nuclear potential well, we can easily see what happens in nuclear
beta-decay, when there is (say) an excess of protons over neutrons in
the nucleus: a proton can release enough energy by becoming a
neutron and dropping into a lower unoccupied neutron state to pay for
the energy required to create the positron and neutrino.
- We may get more information about the nuclear energy levels in a
nucleus by solving the Schroedinger equation for the well in three
dimensions. For simplicity we assume again an infinitely deep well, so
that the wave function of a proton or neutron is completely confined
within a region of radius
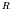 around the origin of coordinates, and
goes to zero on the boundary.
around the origin of coordinates, and
goes to zero on the boundary.
- Because we have assumed that the mean potential in which each
nucleon moves is spherically symmetric, we know that the solution is
separable. As before, we have
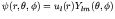 , with the spherical harmonics of definite angular
momentum quantum numbers
, with the spherical harmonics of definite angular
momentum quantum numbers  and
and 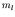 describing the angular
variation, and the radial wave function
describing the angular
variation, and the radial wave function 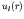 satisfying
satisfying
The boundary conditions are that 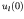 is finite and
is finite and 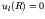 .
.
- For
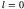 it is easy to verify that the solution is
it is easy to verify that the solution is
with
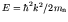 . To satisfy the boundary condition
at
. To satisfy the boundary condition
at 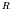 ,
,  must satisfy
must satisfy
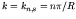 . This condition
defines a series of
. This condition
defines a series of 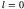 (s-state) energy levels of energies
(s-state) energy levels of energies
- For
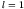 (p states), the Schroedinger equation becomes
(p states), the Schroedinger equation becomes
and the solution is
Again the boundary condition at 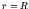 requires
requires
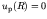 . This condition is satisfied for a series of
. This condition is satisfied for a series of  values; the first
few zeros of
values; the first
few zeros of 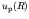 are at
are at
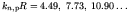 . For each
. For each 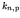 we have a corresponding energy
level
we have a corresponding energy
level 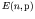 , interleaved with the energy levels of the
s-states.
, interleaved with the energy levels of the
s-states.
- In general, the solutions of the Schroedinger equation for
arbitrary
 are the spherical Bessel functions
are the spherical Bessel functions
For each  , acceptable values of
, acceptable values of  are those which make
are those which make 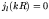 . These zeros of the solution define a series of energy levels,
interleaved with the levels of other values of
. These zeros of the solution define a series of energy levels,
interleaved with the levels of other values of  . In nuclear
physics, we number these levels sequentially for each
. In nuclear
physics, we number these levels sequentially for each  , so the
lowest few energy levels are 1s, 1p, 1d, 2s, 1f, 2p, 1g, 2d, 1h, 3s,
etc. With degeneracy with respect to
, so the
lowest few energy levels are 1s, 1p, 1d, 2s, 1f, 2p, 1g, 2d, 1h, 3s,
etc. With degeneracy with respect to 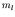 and spin, there are
and spin, there are
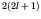 states of the same energy in each level (i.e. this number of
protons and of neutrons may occupy ``one'' energy level).
states of the same energy in each level (i.e. this number of
protons and of neutrons may occupy ``one'' energy level).
- Thus, for this simple model, we find a series of energy levels,
each of which can be occupied by only a limited number of protons and
neutrons, and each of which has definite angular momentum. The
situation is very reminiscent of atomic orbitals.
- This model can be improved in obvious ways, by making the well
finite in depth rather than infinite, and by ``softening'' the outer
boundary somewhat. It is found that these improvements lower the
energy levels (relative to the ground state) somewhat, compared to the
simple well with infinite walls, but do not change the order of
single-nucleon levels much.
- An important test of the shell model is the prediction of
binding energy jumps analogous to those found in atoms for the filled
shell configurations of the noble gases. For atoms, it is observed
that the energy required to ionize a noble gas is three or four times
larger than that required to ionize an atom which has one more
electron than a noble gas (e.g. Ne and Na, Ar and K, Kr and Rb). For
nuclei, a similar phenomenon is observed in several ways.
- Nuclei with certain values of
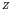 (2, 8, 20, 28, 50, 82, 126)
have unusually large numbers of stable isotopes.
(2, 8, 20, 28, 50, 82, 126)
have unusually large numbers of stable isotopes.
- Similarly, unusually large numbers of isotones are found when
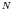 has these same values.
has these same values.
- Nuclei with
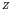 or
or 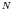 near one of these numbers tend to be more
spherical than usual (i.e. to have relatively small quadrupole
moments).
near one of these numbers tend to be more
spherical than usual (i.e. to have relatively small quadrupole
moments).
- If we plot the energy required to separate the last neutron
from a nucleus as a function of
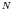 and
and 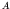 , relatively large
gaps are found at the same numbers mentioned above.
, relatively large
gaps are found at the same numbers mentioned above.
These numbers are usually referred to as magic numbers.
- The simple shell model we have discussed predicts relatively
large energy jumps after filling of the 1s, 1p, 2s, 1f, 2p, 1g, 1h,
and 3p levels, which occur with 2, 8, 20, 34, 40 58, 92, and 138
neutrons or protons. The energy level spacing is thus not
accurately predicted by this version of the shell model.
- The explanation was found independently by Maria Meyer and by
O. Haxel et al in the late 1940's. They assumed that there is a strong
coupling between L and s (note that generally there will be
either zero or one unpaired spin, and
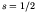 ), so that the
potential seen by a nucleon contains not only the spherically
symmetric term but also a term
), so that the
potential seen by a nucleon contains not only the spherically
symmetric term but also a term
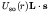 . In this
case,
. In this
case, 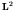 and
and 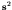 are still good quantum numbers
(conserved) because they commute with
are still good quantum numbers
(conserved) because they commute with
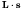 . Total angular
momentum J is of course also conserved. However, since
. Total angular
momentum J is of course also conserved. However, since 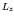 and
and
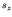 do not commute with
do not commute with
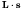 , they are no longer good
quantum numbers. Nuclear states are then labeled with quantum numbers
, they are no longer good
quantum numbers. Nuclear states are then labeled with quantum numbers
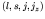 .
.
- The expectation value of
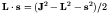 is
is
![$[j(j+1) - l(l+1) - s(s+1)]\hbar^2/2$](img129.gif) , which
has the value
, which
has the value 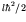 when
when
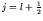 (L and s are
parallel) and
(L and s are
parallel) and
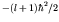 when
when
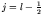 (L and s
anti-parallel). This interaction energy splits each level
(L and s
anti-parallel). This interaction energy splits each level
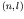 , which is
, which is 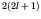 -times degenerate, into two separate levels
that we label
-times degenerate, into two separate levels
that we label
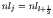 and
and
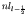 .
.
- By taking the size of the spin-orbit splitting to be quite large
(and opposite to that found in atomic electron clouds), it is possible
to get the energy levels of the nuclear orbital shells to show
splitting at the observed magic numbers.
- The shell model also predicts, for the most part correctly, the
angular momentum of nuclear ground states. To predict these, note that
we expect that all completely filled shells will contribute zero
angular momentum (and positive parity). In partly filled shells, it
appears that nucleons have a strong tendency to form pairs with
opposite
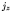 values. Thus even numbers of nucleons in an unfilled
shell still contribute zero angular momentum. The ground state angular
momentum is determined by the remaining unpaired nucleon(s). For
even-
values. Thus even numbers of nucleons in an unfilled
shell still contribute zero angular momentum. The ground state angular
momentum is determined by the remaining unpaired nucleon(s). For
even-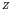 , even-
, even-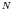 (even-even) nuclei, all nucleons will be paired,
the total angular momentum will be zero, and the parity will be
positive. For odd-even nuclei, the angular momentum
(even-even) nuclei, all nucleons will be paired,
the total angular momentum will be zero, and the parity will be
positive. For odd-even nuclei, the angular momentum 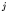 and parity of the
ground state will be those of the single unpaired particle; the parity
will thus be
and parity of the
ground state will be those of the single unpaired particle; the parity
will thus be 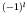 , and the angular momentum will be that of the
shell currently being filled. For odd-odd nuclei, there is no
systematic result.
, and the angular momentum will be that of the
shell currently being filled. For odd-odd nuclei, there is no
systematic result.
- In the shell model, we expect that even-even nuclei will have
all orbital and spin angular momenta paired, so there will be no
residual orbital or intrinsic spin currents, and no magnetic dipole
moment. This prediction is in agreement with experiments.
- For odd-even nuclei, there is one unpaired nucleon. We expect
that this nucleon will contribute a magnetic moment due to its
orbital motion
for a proton, but 0 for a neutron. There will also be a contribution
from the intrinsic spin
where 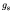 is 5.59 for a proton and
is 5.59 for a proton and 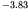 for
a neutron. Since neither L nor s has a defined
z-component, the observed nuclear magnetic dipole moment should be the
projection of the vector sum of the two individual magnetic moment
components along the axis of the one vector defined for the nucleus,
J.
for
a neutron. Since neither L nor s has a defined
z-component, the observed nuclear magnetic dipole moment should be the
projection of the vector sum of the two individual magnetic moment
components along the axis of the one vector defined for the nucleus,
J.
- To calculate the component of
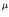 along J, take the dot
product of J with the operator
along J, take the dot
product of J with the operator
giving
Taking the expectation value of both sides of this expression, we find
Now recall that 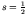 and
and
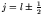 , and find the
expected magnetic moment from the unpaired nucleon to be
, and find the
expected magnetic moment from the unpaired nucleon to be
for
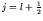 and
and
for
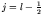 .
.
- These two values are called the ``Schmidt lines'' in a plot of
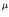 versus
versus 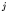 . It is found that the observed magnetic moments
mostly fall between these two values, not on them. This may be due to
mixing of shell model states, or to a change in the intrinsic magnetic
moments of the proton and neutron in the nuclear environment.
. It is found that the observed magnetic moments
mostly fall between these two values, not on them. This may be due to
mixing of shell model states, or to a change in the intrinsic magnetic
moments of the proton and neutron in the nuclear environment.
Nuclear sizes and ground states
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html lec7-nucl_mass.tex
The translation was initiated by on 2002-03-04


2002-03-04

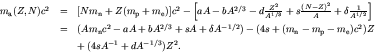
![]() . Each state will
have one neutron and one proton of each spin direction. To estimate
how many states are available, we need a very useful result
concerning the density of states that we have met before.
Consider the solution of the Schroedinger equation in a large
box with sides at
. Each state will
have one neutron and one proton of each spin direction. To estimate
how many states are available, we need a very useful result
concerning the density of states that we have met before.
Consider the solution of the Schroedinger equation in a large
box with sides at ![]() and
and ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and
![]() . The potential is zero inside the box, and infinite outside. In the
box,
. The potential is zero inside the box, and infinite outside. In the
box,