Molecules are of course atoms that are held together by shared valence electrons. That is, most of each atom is pretty much as it would be if the atom were isolated, but one or a few electrons are located in regions (for example, between two atomic cores) where they lead to an overall attractive effect. To see roughly how this works, you might consider the case of two protons and two electrons at the corners of a square. If you calculate (classically) the total electrostatic energy of this arrangement, you will find that it is negative - the system is bound.
Molecules have several kinds of motion, with quite different energy
scales. Assume that a couple of nuclei and a couple of electrons are
confined to a volume with characteristic size ![]() (a couple of Å,
typically). Then the uncertainty principle requires that at a minimum,
(a couple of Å,
typically). Then the uncertainty principle requires that at a minimum,
![]() , so the typical electron energies will be of order
, so the typical electron energies will be of order
The nuclei may also participate in vibrations, in which they interact
directly with the electron cloud. The energies of such motions are
larger than ![]() , and may be estimated by treating the
interaction between electrons and nuclei as simple harmonic motion
with a spring constant
, and may be estimated by treating the
interaction between electrons and nuclei as simple harmonic motion
with a spring constant ![]() , the same (of course) for both parties. In
this case the ratio of electronic (
, the same (of course) for both parties. In
this case the ratio of electronic (![]() ) to nuclear vibrational
energies (
) to nuclear vibrational
energies (![]() ) will be of order
) will be of order
Consider the Schrödinger equation for a system of two identical
nuclei and two electrons, in the centre of mass system of the nuclei,
neglecting spin:
We will solve this system by a separation and some approximations.
Because the electrons are much lighter than the nuclei, the
nuclei will hardly move at all in the time that an electron takes to
``orbit'' once, so let's suppose that we can solve the simpler problem
of electron motion in the presence of motionless nuclei separated by a
fixed ![]() , for which the electronic wave equation is
, for which the electronic wave equation is
To find equations satisfied by the ![]() 's, put
's, put ![]() into
the exact Schrödinger equation and projects using each of the
into
the exact Schrödinger equation and projects using each of the
![]() 's:
's:
We now make the adiabatic or Born-Oppenheimer
approximation by assuming that we can neglect
![]() compared to
compared to
![]() . In this case, we get the nuclear
wave equation
. In this case, we get the nuclear
wave equation
The equation for ![]() is in the form of a wave equation with the
function
is in the form of a wave equation with the
function ![]() playing the role of potential energy. Let us
consider the specific case of the electrons in a state of zero orbital
angular momentum. In this case,
playing the role of potential energy. Let us
consider the specific case of the electrons in a state of zero orbital
angular momentum. In this case,
![]() is a function
only of the radial variable
is a function
only of the radial variable ![]() , and the wave equation for
, and the wave equation for ![]() becomes one for a spherically symmetric potential. In this case, the
Hamiltonian commutes with
becomes one for a spherically symmetric potential. In this case, the
Hamiltonian commutes with ![]() and
and ![]() . The simultaneous
eigenfunctions of these operators are the spherical harmonics, and
have eigenvalues
. The simultaneous
eigenfunctions of these operators are the spherical harmonics, and
have eigenvalues ![]() and
and ![]() .
.
Since there is no privileged direction in space, the total energy of
the system cannot depend on ![]() , but it does depend on
, but it does depend on ![]() . (You may
wonder why the direction of
. (You may
wonder why the direction of ![]() is not a privileged direction
now. It is for the electron cloud, but in a spherically symmetric
electron potential, it is just a coordinate as far as the nuclei are
concerned. Thus
is not a privileged direction
now. It is for the electron cloud, but in a spherically symmetric
electron potential, it is just a coordinate as far as the nuclei are
concerned. Thus ![]() can rotate in space, and the nuclei may have
non-zero angular momentum.) It will be found that there is also
another quantum number in the system,
can rotate in space, and the nuclei may have
non-zero angular momentum.) It will be found that there is also
another quantum number in the system, ![]() , which acts as a principal
quantum number and will be found to number vibrational states. Thus we
may write (dividing the radial function by
, which acts as a principal
quantum number and will be found to number vibrational states. Thus we
may write (dividing the radial function by ![]() to get a simple form
for the resulting equation)
to get a simple form
for the resulting equation)
Now in a bound molecular state, the energy ![]() varies from the
sum of the energies of the two atoms separately for large
varies from the
sum of the energies of the two atoms separately for large ![]() , through
a local minimum, to a large positive value as the two nuclei get close
to one another. We may approximate the minimum region of
, through
a local minimum, to a large positive value as the two nuclei get close
to one another. We may approximate the minimum region of ![]() by a
second order expansion:
by a
second order expansion:
For the electron cloud, the (slowly rotating) internuclear axis ![]() picks out a direction in space which we take as the
picks out a direction in space which we take as the ![]() -axis. The
electronic structure of the molecule is invariant under rotation
around this axis, so
-axis. The
electronic structure of the molecule is invariant under rotation
around this axis, so ![]() commutes with
commutes with ![]() . However,
. However, ![]() ,
,
![]() and
and ![]() do not commute with
do not commute with ![]() . The electronic eigenstates
. The electronic eigenstates
![]() of
of ![]() may also be made to be eigenstates of
may also be made to be eigenstates of ![]() , so that
, so that
Diatomic molecules are symmetric to reflections through planes
including ![]() , such as the
, such as the ![]() plane. Thus if operator
plane. Thus if operator ![]() does this,
does this,
If ![]() is 0, the state is not degenerate, and
is 0, the state is not degenerate, and ![]() can
only multiply it by a constant. Since
can
only multiply it by a constant. Since ![]() , such states are
either symmetric or anti-symmetric to reflection through a plane, and
one distinguishes
, such states are
either symmetric or anti-symmetric to reflection through a plane, and
one distinguishes ![]() and
and ![]() states.
states.
If the molecule has two nuclei with identical charge (a homonuclear
molecule), the centre is also a symmetry point, and states have
parity. States of even (g) and uneven (u) parity are denoted by
![]() ,
,
![]() , etc. A homonuclear diatomic molecule
has four non-degenerate sigma states,
, etc. A homonuclear diatomic molecule
has four non-degenerate sigma states,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
.
Finally, each electronic eigenstate has a total spin ![]() , with
eigenvalues of
, with
eigenvalues of ![]() of
of
![]() . The value of
. The value of ![]() is given as a left superscript (the multiplicity) on the
designation. Thus, since most molecular ground states (often labelled
X) are
is given as a left superscript (the multiplicity) on the
designation. Thus, since most molecular ground states (often labelled
X) are ![]() states of zero total spin, the complete label for a
ground state could be X
states of zero total spin, the complete label for a
ground state could be X![]() or X
or X
![]() .
.
We may start our study of electronic wave functions with the simplest
molecule of all, H![]() , with two protons and one electron. To
simplify writing, we will switch to Hartree's dimensionless atomic units, in which the units of mass, charge, angular momentum,
and length are chosen to be
, with two protons and one electron. To
simplify writing, we will switch to Hartree's dimensionless atomic units, in which the units of mass, charge, angular momentum,
and length are chosen to be ![]() ,
, ![]() ,
, ![]() , and
, and
![]() , with
the result (you may check this) that the units for time, velocity, and
energy become
, with
the result (you may check this) that the units for time, velocity, and
energy become
![]() ,
,
![]() , and
, and
![]() ,
where
,
where ![]() is the ground state binding energy of H. In these units,
the electronic wave equation becomes
is the ground state binding energy of H. In these units,
the electronic wave equation becomes
We will solve this equation using the simple approximation of a linear
combination of atomic orbitals (LCAO). If the nuclei are far apart,
the electron will be attached to one (say A), with wave function
The numerator is
This problem may be solved exactly (although numerically, not analytically) through the use of confocal elliptic coordinates, which are also used in the evaluation of the two-centre integrals.
With two electrons, we must consider the effects of the exclusion principle, which states that eigenstates must be antisymmetric to exchange of two identical fermions. The eigenstates of the two-electron cloud are products of spatial wave functions and spin functions. How does the spin affect the situation?
The total spin operator is
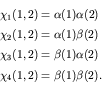
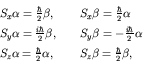
It is easily shown that ![]() has eigenvalues of
has eigenvalues of ![]() and
and
![]() of
of ![]() and
and ![]() , while
, while ![]() has
has ![]() and
and ![]() . We
now have four normalized and orthogonal spin eigenstates that we will
denote by
. We
now have four normalized and orthogonal spin eigenstates that we will
denote by ![]() for clarity.
for clarity. ![]() is antisymmetric to
particle exchange, while the other three states are symmetric. We call
the one
is antisymmetric to
particle exchange, while the other three states are symmetric. We call
the one ![]() state a spin singlet, while the other three states form
a spin triplet.
state a spin singlet, while the other three states form
a spin triplet.
In solving (approximately) the problem of the electron cloud structure
for the two-electron system H![]() , we have the obvious choice of using
as a basis set the molecular orbitals found for H
, we have the obvious choice of using
as a basis set the molecular orbitals found for H![]() , or the atomic
orbitals of the individual H atoms. Either provides a useful basis for
solution. We will start with the molecular orbitals.
, or the atomic
orbitals of the individual H atoms. Either provides a useful basis for
solution. We will start with the molecular orbitals.
Recall that we have two molecular orbitals ![]() and
and
![]() (which are even and odd under reflection through the
midpoint of
(which are even and odd under reflection through the
midpoint of ![]() ). The product
). The product
![]() is symmetric under exchange of electrons 1 and 2, as are the
combinations
is symmetric under exchange of electrons 1 and 2, as are the
combinations
![]() and
and
![]() . On
the other hand, the function
. On
the other hand, the function
![]() is antisymmetric under
exchange of the electrons. Thus we may form (only) four orthogonal
eigenfunctions that are antisymmetric under exchange:
is antisymmetric under
exchange of the electrons. Thus we may form (only) four orthogonal
eigenfunctions that are antisymmetric under exchange:
![\begin{displaymath}\begin{array}{l}
\Phi_{\rm A}(1,2) = \Phi_{\rm g}(1)\Phi_{\r...
...i_{\rm u}(1)\Phi_{\rm u}(2)]\chi_{1,M_S}(1,2), \\
\end{array} \end{displaymath}](img157.gif)
To get a bonding state, we need the two electrons to prefer to be
between the two protons. If they both occupy the bonding orbitals of
the H![]() system, and have opposite spins (so that the exclusion
principle will not require them to occupy different spatial states),
we guess that we should get maximum bonding. Thus we guess that
system, and have opposite spins (so that the exclusion
principle will not require them to occupy different spatial states),
we guess that we should get maximum bonding. Thus we guess that
![]() may a reasonable approximation to the ground state
of H
may a reasonable approximation to the ground state
of H![]() .
.
We now need to solve the equation
If one uses the approximate LCAO molecular orbitals found above, the
binding energy ![]() is calculated to be 2.68 eV (compared to an
accurate value of 4.75 eV), with a computed equilibrium
is calculated to be 2.68 eV (compared to an
accurate value of 4.75 eV), with a computed equilibrium ![]() of 0.8
Å, compared to an accurate value of 0.74 Å.
of 0.8
Å, compared to an accurate value of 0.74 Å.
The trial wavefunction that we have used may be written as the sum of
two terms,
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html lec4-mol_struct.tex
The translation was initiated by on 2002-01-28