Several-particle systems and approximation methods

Several-particle systems

Introduction

Consider a system of $N$ spinless particles of masses $m_i$, positions ${\bf r_i}$ and momenta ${\bf p_i}$. The Schroedinger equation for this system is an obvious generalization of the one for a single particle:

$$i\hbar \frac{\partial}{\partial t} \Psi = \left[ \sum_{i=1}^N... ...{r_i}^2\right) + V({\bf r_1},...,{\bf r_N}, t) \right] \Psi,$$

where $\nabla_{r_i}$ acts only on the coordinates of the $i$th particle, and the wave function $\Psi$ is a function of coordinates of all the particles and of time.

All the components of position and momentum of particle $i$ commute with with the coordinates of particle $j$.

Two-body systems

A system of particular interest is one composed of two bodies of masses $m_1$ and $m_2$ which interact via a potential $V({\bf r_1} - {\bf r_2})$ that depends only on the relative positions of the two particles. For this system, the Schroedinger equation is

$$i\hbar \frac{\partial}{\partial t} \Psi({\bf r_1},{\bf r_2},t... ... + V({\bf r_1}-{\bf r_2}) \right] \Psi({\bf r_1},{\bf r_2},t).$$

Define the relative separation vector

$${\bf r = r_1 - r_2}$$

and the position of the centre of mass

$${\bf R} = \frac{m_1{\bf r_1}+m_2{\bf r_2}}{m_1+m_2}.$$

Changing variables, the Schroedinger equation becomes

$$i\hbar \frac{\partial}{\partial t} \Psi({\bf R},{\bf r},t) =... ...mu}\nabla_{r}^2 + V({\bf r}) \right] \Psi({\bf R},{\bf r},t),$$

with total mass $M=m_1 + m_2$ and reduced mass

$$\mu = \frac{m_1 m_2}{m_1 + m_2}.$$

Following the usual method for solving partial differential equations, assume that the solution is separable. Start by separating off the time:

$$\Psi({\bf R},{\bf r},t) = \Pi({\bf R},{\bf r}) \Theta(t).$$

Upon substitution, we find

$$\frac{i\hbar}{\Theta(t)}\frac{{\rm d}}{{\rm d} t} \Theta(t) ... ...2\mu}\nabla_{r}^2 + V({\bf r}) \right] \Pi({\bf R},{\bf r}).$$

Since the right hand side is a function only of ${\bf R}$ and ${\bf r}$, while the left is a function only of $t$, both must be equal to a constant $E_{\rm tot}$, the total energy of the system. The time equation clearly has the solution

$$\Theta(t) = \exp(-iE_{\rm tot}t/\hbar),$$

where we are leaving the normalization to the space functions.

Next we separate the two space coordinates, assuming

$$\Pi({\bf R},{\bf r}) = \Phi({\bf R}) \psi({\bf r}).$$

We find

$$E_{\rm tot} = -\frac{1}{\Phi({\bf R})} \frac{\hbar^2}{2M} \... ...}{2\mu} \nabla_{\bf r}^2 + V({\bf r}) \right] \psi({\bf r}).$$

The two terms on the right depend on different variables, and hence must each be separately constant. Call their constant values $E_{\rm CM}$ and $E$. We see at once that $E_{\rm tot} = E_{\rm CM} + E$, as expected, and we get two more equations:

$$- \frac{\hbar^2}{2M} \nabla_{\bf R}^2 \Phi({\bf R}) = E_{\rm CM} \Phi({\bf R}),$$

and

$$\left[ -\frac{\hbar^2}{2\mu} \nabla_{\bf r}^2 + V({\bf r}) \right] \psi({\bf r}) = E \psi({\bf r}).$$

The centre of mass equation describes the motion of a free particle of mass $M$ and energy $E_{\rm CM}$. The equation for relative motion is the same as the Schroedinger equation of a single particle of mass $\mu$ moving in the potential $V({\bf r})$. Thus as long as we work in the centre of mass coordinates of the two-body system, we do not need to be concerned about its centre of mass motion.

Indistinguishable particles

We have already seen that the parity operator commutes with a spherically symmetric Hamiltonian, so eigenstates of such a system are also parity eigenstates. With several particles, it is interesting to consider another exchange operator: the interchange operator $P_{ij}$ which exchanges the space and spin coordinates of particle $i$ with that of particle $j$. If these particles are identical this operator must commute with the Hamiltonian.

Since two successive interchanges restore the original situation, the eigenvalues $\epsilon$ of the interchange operator must be $\pm 1$. A wave function with $\epsilon = +1$ is called symmetric under interchange; the opposite is antisymmetric.

If we perform a series of interchanges, we do not usually come back to the original configuration. Further, a series of interchanges do not in general mutually commute, since doing permutations in different orders leads to different rearrangements of particles. Hence an arbitrary series of interchanges does not commute with the system Hamiltonian, and is not a constant of motion.

However, two particular kinds of states have simple behaviour under all series of permutations. If the state is symmetric under all interchanges, or antisymmetric under all interchanges, it does commute with $H$ and is a constant of the motion.

It appears that all systems of identical particles are one of these types. Particles totally symmetric under interchange are bosons and have integral spin (e.g. photons); particles with totally antisymmetric wave functions are fermions and have half-integral spin (e.g. electrons).

The requirement that the wave function of a system of fermions be totally antisymmetric under interchange is a general form of the Pauli exclusion principle. It turns out to have important, observable consequences for systems such as H$_2$, for which the wave function must be antisymmetric under exchange of the two electrons, and under exchange of the two protons.

Approximation methods

There are many interesting cases in nature in which a system that we can model (at least approximately) can be slightly altered (for example by imposing a ``weak'' external electric or magnetic field). It is often possible to describe the effect of this extra influence by considering how the basic eigenstates and eigenvalues are perturbed. This topic covers a large range of important and very useful methods of understanding quantum systems.

Time-independent perturbation theory

Consider the discrete states of a Hamiltonian

$$H = H_0 + \lambda H',$$

where we know the eigenstates $\psi_k$ of $H_0$, and $\lambda H'$ is a small perturbation. $\lambda$ is a strength parameter that we will use to distinguish between various orders of approximation. We are looking for approximate solutions of

$$H \Psi_k = {\cal E}_k \Psi_k.$$

Suppose the unperturbed energy levels are not degenerate. (The degenerate case is dealt with in B & J.) We expand the wave functions and energies we want, $\Psi_k$ and ${\cal E}_k$, in a series of powers of the perturbation parameter $\lambda$:

$$\Psi_k = \sum_{n=0}^\infty \lambda^n \psi_k^{(n)}$$

and

$${\cal E}_k = \sum_{n=0}^\infty \lambda^n E_k^{(n)}.$$

The functions $\psi_k^{(n)}$ and values $E_k^{(n)}$ are initially unknown; we must determine them.

Substitute into the full Schroedinger equation and equate the terms with equal powers of $\lambda$ on the two sides of the equation. For the term $\lambda^0$, we find

$$H_0 \psi_k^{(0)} = E_k^{(0)} \psi_k^{(0)},$$

so the leading term in our expansion is just the eigenstates and eigenvalues of the unperturbed problem, as expected. The next term gives

$$H_0 \psi_k^{(1)}+H' \psi_k = E_k \psi_k^{(1)}+E_k^{(1)}\psi_k$$

and so on. To use this equation, left multiply the equation by $\psi_k^\star$ and integrate. We find

$$\langle \psi_k \vert H_0 - E_k \vert \psi_k^{(1)} \rangle + \langle \psi_k \vert H' - E_k^{(1)} \vert \psi_k \rangle = 0.$$

When we use the Hermitian nature of $H_0$ to make it operate on the left wave function, the left term vanishes, so we get the simple result

$$E_k^{(1)} = \langle \psi_k \vert H' \vert \psi_k \rangle \equiv H_{kk}'.$$

Similarly,

$$E_k^{(2)} = \langle \psi_k \vert H' - E_k^{(1)} \vert \psi_k^{(1)} \rangle.$$

This is a typical result of perturbation theory: the answers contain matrix elements such as $H_{kk}'$.

But how to get $\psi_k^{(1)}$? Expand it in the complete set of solutions of the unperturbed problem, which we know:

$$\psi_k^{(1)} = \sum_m a_m^{(1)} \psi_m.$$

Putting this into the first-order equation,

$$(H_0 - E_k) \sum_m a_m^{(1)} \psi_m + (H' - E_k^{(1)}) \psi_k = 0.$$

Left multiply by $\psi_l^\star$ and integrate over space:

$$a_l^{(1)} (E_l - E_k) + \langle \psi_l \vert H' \vert \psi_k \rangle - E_k^{(1)} \delta_{kl} = 0.$$

For $l = k$ we get back the expression for $E_k^{(1)}$. For other values of $l$ we have

$$a_l^{(1)} = \frac{H_{lk}'}{E_k - E_l}.$$

Since $a_k^{(1)}$ is undetermined, we set it to 0. With this result for the expansion coefficients, we can determine the first-order correction $\psi_k^{(1)}$ to the unperturbed eigenstates. We can also evaluate the second-order energy correction $E_k^{(2)}$:

$$E_k^{(2)} = \sum_{m \neq k} \frac{\vert H_{km}'\vert^2}{E_k - E_m}.$$

If the unperturbed levels are degenerate, we get more bookkeeping complexity, but similar results.

Time-dependent perturbation theory

Next consider the case in which the total Hamiltonian is mainly a system in a steady state, but is slightly perturbed by some time-dependent effect:

$$H = H_0 + \lambda H'(t).$$

Now suppose we know the $E_k$'s and $\psi_k$'s of the stationary problem, so that $H_0 \psi_k = E_k \psi_k$. The solution to the time-dependent Schroedinger equation for the unperturbed system

$$i \hbar \frac{\partial \Psi_0}{\partial t} = H_0 \Psi_0$$

is

$$\Psi_0 = \sum_k c_k^{(0)} \psi_k e^{-iE_k t/\hbar}.$$

The $c_k^{(0)}$'s are constants. Since the $\psi_k$'s form a complete set, we can expand the general solution of the time-dependent problem (with $H$ in place of $H_0$) as

$$\Psi = \sum_k c_k(t) \psi_k e^{-iE_k t/\hbar}.$$

Here $c_k(t)$ is probability amplitude of finding the state in state $k$ at time $t$; $c_k^{(0)}$ is the initial value of $c_k(t)$.

To find the $c_k(t)$, insert the expansion into the time-dependent Schroedinger equation, and use the fact that $H_0 \psi_k = E_k \psi_k$:

$$\begin{array}{ll} i\hbar \sum_k \dot{c}_k(t) \psi_k e^{-iE_k... ...m_k c_k(t) \lambda H' \psi_k e^{-iE_k t/\hbar} \\ \end{array}$$

so that

$$i\hbar \sum_k \dot{c}_k(t) \psi_k e^{-iE_k t/\hbar} = \sum_k c_k(t) \lambda H' \psi_k e^{-iE_k t/\hbar}.$$

Multiplying from the left by a particular $\psi_b$ and integrating, we find

$$\dot{c}_b(t) = (i\hbar)^{-1} \sum_k \lambda H_{bk}'(t) c_k(t) e^{-i \omega_{bk} t}$$

where $\omega_{bk} = (E_b - E_k)/\hbar$ and $H_{bk}' = \langle \psi_b \vert H'(t) \vert \psi_k \rangle$. So far, this is equivalent to the original formulation. Because the perturbation is weak, expand the $c_k$'s in a series in $\lambda$ as

$$c_k(t) = c_k^{(0)}(t) + \lambda c_k^{(1)}(t) + \lambda^2 c_k^{(2)}(t) + ...$$

Substituting into the equation for $\dot{c}_b$ and (as usual) equating coefficients of equal powers of $\lambda$, we obtain

$$\dot{c}_b^{(0)} = 0$$

$$\dot{c}_b^{(1)} = (i\hbar)^{-1} \sum_k H_{bk}'(t) e^{i \omega_{bk}t} c_k^{(0)}$$

and so on. Each successive term in the series expansion for $c_b$ (which may be any of the $c_k$'s) can be integrated from the already determined variation of the next lower order term. The first equation is consistent with our assumption that with no perturbation ($\lambda = 0$), the $c_k$'s are constant. Let's assume now that only one of the $c_k$'s is initially non-zero (for all $t < t_0$), so the system is in the well-defined state $c_a^{(0)} = 1$, and that the perturbation is first turned on at $t = t_0$. We then may compute how the other $c_k$'s increase from zero as a result of transitions induced by the perturbation. For a particular state $b$,

$$c_b^{(1)}(t) = (i\hbar)^{-1} \int_{t_0}^t H_{ba}'(t') e^{i \omega_{ba} t'} {\rm d}t',$$

and the probability of finding the system in state $b$ at $t$ is

$$P_{ba}(t) = \vert c_b^{(1)}(t) \vert^2.$$

We can obtain a widely useful result from this reasoning. Suppose that the perturbation $H'$ is constant except for being turned on at $t_0 = 0$. At time $t$ the expansion coefficient $c_b^{(1)}(t)$ is given by

$$c_b^{(1)}(t) = -\frac{H_{ba}'}{\hbar \omega_{ba}} (e^{i \omega_{ba} t} - 1),$$

and the probability that a transition from $a$ to $b$ has occurred at $t$ is

$$P_{ba}(t) = \vert c_b^{(1)} (t)\vert^2 = \frac{2}{\hbar^2} \vert H_{ba}'\vert^2 F(t,\omega_{ba})$$

where $F(t,\omega) = (1 - \cos \omega t)/\omega^2$. $F(t,\omega)$ is a function that is sharply peaked around $\omega = 0$, where it has the value $t^2/2$, and is nearly zero at values of $\omega$ farther from 0 than $\pm 2 \pi/t$.

Now suppose that the transition from the initial isolated state $a$ is to a group of neighboring states (for example in a free particle continuum) around the final energy $E_b$. Take the density of states - the number of states $b'$ per unit energy around $E_b$ that are accessible from $a$ - to be $\rho_{b'}(E_{b'})$. Then the first-order probability of transition from $a$ to one of the states around $b$ is

$$P_{ba}(t) = \frac{2}{\hbar^2} \int_{E_b - \eta}^{E_b + \eta} ... ...b'a}\vert^2 F(t,\omega_{b'a}) \rho_{b'}(E_{b'}) {\rm d}E_{b'},$$

where $\eta$ is large enough to cover essentially all the region where the sharply peaked function $F(t,\omega)$ is non-zero. Assuming that $H_{b'a}'$ and $\rho_{b'a}$ do not vary much within the integration range, we may remove them from inside the integral and extend the limits to $\pm \infty$. The result is

$$\begin{array}{lll} P_{ba}(t) & = & \frac{2}{\hbar^2} \vert H... ...\hbar} \vert H_{ba}\vert^2 \rho_{b}(E_{b}) t. \\ \end{array}$$

Defining the probability of transition per unit time $W_{ba} \equiv {\rm d} P_{ba} / {\rm d} t$, we finally obtain the widely applicable result known as Fermi's Golden Rule,

$$W_{ba} = \frac{2\pi}{\hbar} \vert H_{ba}\vert^2 \rho_{b}(E_{b}),$$

which simply states that the probability per unit time of the transition from $a$ to one of the states $b$ is proportional to a transition matrix element squared times the density of final states. Although we have proved this for a very specific case, we will find that it is also true in certain cases in which radiation interacts with atoms, and in some nuclear processes.

Variational estimation of bound state energies

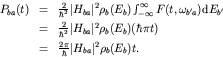
As a final topic, we briefly look at a non-perturbation technique for finding (often usefully accurate) upper bounds to bound state energy levels. In this technique we use parameterized approximate wave functions, and vary the parameters to obtain the best estimate possible with our chosen functions; the technique is therefore called the variational method.

Consider again a system with a Hamiltonian $H$, eigenfunctions $\psi_k$, and (some) discrete energy eigenvalues $E_k$. We assume that we do not know the solution to this problem even though a solution exists, but it helps a lot if we have some idea of the general form of the wave functions of low-lying states.

Pick a trial function $\phi$ that has one or several free parameters and that is convenient to manipulate; if possible it should have a form something like the expected wave function of the ground state. Form the functional

$$E[\phi] = \frac{\langle \phi \vert H\vert \phi \rangle} {\langle \phi \vert \phi \rangle}.$$

This functional provides an upper bound the the exact ground state energy $E_0$. This is easily seen by expanding the trial function in the complete orthonormal set of eigenstates of the system (we don't know these, so our expansion at this point is simply formal):

$$\phi = \sum_n a_n \psi_n.$$

Substituting into the functional $E[\phi]$, carrying out the required integration over space coordinates, and using the fact that the $\psi_n$ are eigenstates of $H$, we find

$$E[\phi] = \frac{\sum_n \vert a_n\vert^2 E_n}{\sum_n \vert a_n\vert^2}.$$

Now subtract the ground state energy $E_0$ from both sides to get

$$E[\phi] - E_0 = \frac{\sum_n \vert a_n\vert^2 (E_n - E_0)} {\sum_n \vert a_n\vert^2}.$$

Because $E_n \geq E_0$, the right-hand side is $\geq 0$, and we see that $E[\phi]$ is indeed an upper bound for $E_0$.

The Rayleigh-Ritz variational method consists simply of choosing a suitable parameterized trial function and minimizing $E[\phi]$ with respect to these parameters in order to get the best possible estimate of the ground state energy. If the trial function is chosen with care, quite respectable estimates of ground state energy are possible.

This method may also be used to obtain an estimate of the energy of an excited state provided one can find a trial function that is orthogonal to all states below the one of interest. To see this, arrange the energy eigenstates in order of increasing energy. If the trial function is orthogonal to the lowest $i$ states of the system, we have $a_n = \langle \phi \vert \psi_n \rangle = 0$ for $n = 1, 2, ... i$ and the expansion becomes

$$E[\phi] - E_{i+1} = \frac{\sum_{n=i+1} \vert a_n\vert^2 (E_n - E_{i+1})} {\sum_{n=i+1} \vert a_n\vert^2},$$

and again we see that the right-hand side is non-negative.

This result is most useful, at least for a few low-lying states, if the eigenstates of the problem are known to have symmetry properties such as parity or angular momentum. For example, if the state of interest has a different angular momentum than all of the states below it, the trial function may be chosen to have this angular momentum and is automatically orthogonal to the lower states. Similarly, the energy of a first excited state of opposite parity to the ground state may be estimated by using a trial function of opposite parity to that of the ground state.

About this document ...

Several-particle systems and approximation methods

This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.46)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html lec2-approx.tex

The translation was initiated by on 2002-01-14