

Beta and gamma decays
- Beta decay is one of the most easily found kinds of
radioactivity. As we have seen, this result of the weak interaction
leads to conversion of a neutron into a proton or vice versa, with the
necessary charge change being made possible by the emission of a
positive or negative beta particle (positron or electron). To ensure
conservation of lepton number, each such event is accompanied by
emission of an electron neutrino. Alternatively, an orbital electron
may be absorbed (electron capture or K-capture), changing a proton
into a neutron (this process competes with
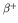 emission), with
emission of an electron neutrino.
emission), with
emission of an electron neutrino.
- The spectra of electrons or positrons emitted in beta decay is
a continuum of energies, up to a maximum value, with most emitted
betas having intermediate energies. The emitted, unobserved, neutrinos
also have a continuous energy distribution. In K-capture, there is no
electron emitted; the neutrino is mono-energetic. (Mono-energetic
electrons also emerge from de-excitation of an excited nucleus by internal
conversion [see below]; this process leads to electron emission but is
quite a different physical mechanism than beta decay.)
- We can predict the general form of the energy spectrum of the
(observable) beta particle, but not the absolute decay rate, from a
simple theory proposed by Fermi. The form of the spectrum is found
simply by considering the density of final states!
- We have seen, using perturbation theory, that the probability
per unit time of a transition into a group of closely spaced states is
given by
where
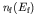 is the density of final states and
is the density of final states and
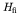 is the matrix element of the Hamiltonian between states
is the matrix element of the Hamiltonian between states
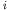 and
and 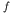 (Lecture 2).
(Lecture 2).
- In beta decay of an even-odd nucleus, the initial state is
simply the wave function of the single odd nucleon (let's say it is a
proton),
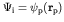 . The final
state is the wave function of the new neutron, the emitted
positron and the neutrino:
. The final
state is the wave function of the new neutron, the emitted
positron and the neutrino:
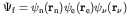 . The
interaction Hamiltonian is uncertain, but very short range, and Fermi
tried the simplest operator he could think of, namely a constant that
we will call
. The
interaction Hamiltonian is uncertain, but very short range, and Fermi
tried the simplest operator he could think of, namely a constant that
we will call 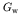 . Thus the matrix element is only non-zero to
the extent that the initial and final wave functions overlap:
. Thus the matrix element is only non-zero to
the extent that the initial and final wave functions overlap:
- For the lepton wave functions we take plane waves (although
this is not accurate for the beta particle, which is affected by the
Coulomb interaction with the nuclear protons). These must be
normalized, so we again introduce an artificial (large) volume
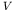 :
:
and
- Now for lepton energies of a few MeV or less, the wavelengths of
the lepton wave function are of order 1 MeV/
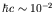 fm
fm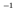 . Thus the exponent of each of the exponentials is small over
the extent of the nucleus, and we may replace the two lepton wave
functions by
. Thus the exponent of each of the exponentials is small over
the extent of the nucleus, and we may replace the two lepton wave
functions by 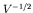 . Then our trial matrix element is just
. Then our trial matrix element is just
In general we do not know what the value of the integral is. Let us
simply assume that it does not depend on how the released energy is
partitioned between the outgoing beta particle and the neutrino, so
that for a given decay we may treat it as a constant which we will
call 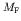 .
.
- We have so far ignored the (significant) effect of the Coulomb
interaction between the outgoing beta particle and the nucleus. The
effect of this interaction for non-relativistic particles is to
replace the beta particle plane wave at the origin by the wavefunction
of the beta particle in the electric field of the daughter nucleus of
charge
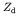 . This is equivalent to multiplying our expression
for
. This is equivalent to multiplying our expression
for 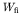 by
by
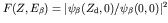 . It is found that
. It is found that
where
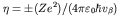 and
the sign of
and
the sign of 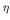 is opposite to that of the charge on the beta
particle. For both electrons and positrons
is opposite to that of the charge on the beta
particle. For both electrons and positrons
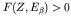 ; for
large beta velocity this factor approaches 1 (as it should) but for
small
; for
large beta velocity this factor approaches 1 (as it should) but for
small 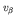 the function tends to a large value for electrons (for
which the outgoing wavefunction is concentrated around the nucleus)
and to a small value for positrons (for which the outgoing
wavefunction is made small near the nucleus by the Coulomb repulsion).
the function tends to a large value for electrons (for
which the outgoing wavefunction is concentrated around the nucleus)
and to a small value for positrons (for which the outgoing
wavefunction is made small near the nucleus by the Coulomb repulsion).
- So finally the decay rate that we need is
- What density of final states is needed? After the decay, we may
suppose that the final nuclear state is stable, so it has a
well-defined energy, while the initial unstable state has finite width
due to the uncertainty principle
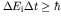 . Suppose that in the decay we can measure precisely the state
of the outgoing electron (its momentum vector, not its position, of
course). Now because of the uncertainty in initial energy, the
outgoing neutrino with have a slightly uncertain energy, and may end
up in any one of a number of closely adjacent states. Thus for the
probability of decay to a specific final electron state, we need the
density of final neutrino states.
. Suppose that in the decay we can measure precisely the state
of the outgoing electron (its momentum vector, not its position, of
course). Now because of the uncertainty in initial energy, the
outgoing neutrino with have a slightly uncertain energy, and may end
up in any one of a number of closely adjacent states. Thus for the
probability of decay to a specific final electron state, we need the
density of final neutrino states.
- Now recalling that the neutrino is relativistic (and may have
non-zero mass), so that its momentum and energy are related by
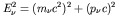 , we may use our earlier result
that the density of plane wave states (neglecting spin) in
, we may use our earlier result
that the density of plane wave states (neglecting spin) in 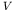 is
is
![$n_{\rm f} = [V/(2 \pi)^3]4 \pi k^2_\nu {\rm d}k_\nu$](img30.gif) , where
, where
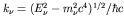 and
and
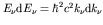 . Thus the relativistic density of
neutrino states is
. Thus the relativistic density of
neutrino states is
- However, because the outgoing neutrino is not observable, we
need to express this in terms of the observable beta particle energy,
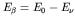 , where
, where 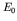 is the total energy available for
the decay. Thus the probability of decay into a single electron state
of energy
is the total energy available for
the decay. Thus the probability of decay into a single electron state
of energy 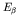 is
is
and the total probability of decay into any of the final beta
particle states within momentum interval
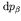 - using
now the density of beta particle states - is
- using
now the density of beta particle states - is
The distribution of electron energies (or momenta) is produced
entirely by the density of states factors.
- This theory of beta decay is usually tested, and the value of
the total decay energy determined accurately, by plotting the value of
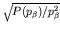 against the total or kinetic
energy. Such a plot is called a Kurie plot; it has the virtue
that if
against the total or kinetic
energy. Such a plot is called a Kurie plot; it has the virtue
that if 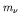 is small, the measured points are proportional to
is small, the measured points are proportional to
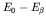 and the graph crosses 0 where
and the graph crosses 0 where 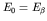 . From such
graphs it is found that the rest mass-energy of the neutrino is no
more than about 5 eV.
. From such
graphs it is found that the rest mass-energy of the neutrino is no
more than about 5 eV.
- The total transition rate for a decay is found by integrating
the expression above over beta particle energy. The resulting mean
lifetime of a beta-unstable nucleus is
where
neglecting the neutrino mass. The function
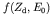 is
dimensionless and has been extensively tabulated. Once the value of
the constant
is
dimensionless and has been extensively tabulated. Once the value of
the constant 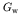 has been determined (from an experiment in
which the matrix element can be evaluated approximately), other
experiments determine experimentally the value of the unknown matrix
elements of the decay in terms of the quantity
has been determined (from an experiment in
which the matrix element can be evaluated approximately), other
experiments determine experimentally the value of the unknown matrix
elements of the decay in terms of the quantity
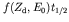 . This ft-value is the quantity usually quoted for an
experimentally studied beta decay, rather than the value of the matrix
element.
. This ft-value is the quantity usually quoted for an
experimentally studied beta decay, rather than the value of the matrix
element.
- A process that competes with positron beta decay is electron
capture, in which the same conversion of a proton into a neutron is
accomplished by the capture of an orbital electron with emission
of a neutrino. We may calculate the rate of this process using very
similar reasoning to that discussed above.
- Again we use Fermi's golden rule. Now the initial state is a
nuclear proton wave function and an orbital electron wave function,
while the final state is an nuclear neutron and a free neutrino of
(almost) definite energy (the initial state, of finite lifetime, has a
slightly uncertain energy). The initial electron state (assuming the
electron to be a K electron in the innermost shell) is thus
Thus the total rate for this process is
where the initial 2 arises because there are two K-shell electrons,
the matrix element is given by
and the density of states is only that of the neutrino,
Because the electron wave function is normalized to its confined
volume around the nucleus, 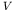 only appears to the first power
now. Again we simply need to evaluate the electron wave function at the
nucleus (i.e. at
only appears to the first power
now. Again we simply need to evaluate the electron wave function at the
nucleus (i.e. at 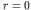 ), and the only part of the matrix element
that we cannot evaluate is the nuclear overlap integral, which is the
same integral
), and the only part of the matrix element
that we cannot evaluate is the nuclear overlap integral, which is the
same integral 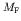 that appears in the normal beta decay
theory.
that appears in the normal beta decay
theory.
- Putting the pieces together, the transition rate for electron
capture (the inverse of the lifetime) is
where 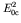 is the energy available in the decay (given to
the escaping neutrino). Note that this result is two times larger
than in C & G because they have calculated the rate for a single K
electron.
is the energy available in the decay (given to
the escaping neutrino). Note that this result is two times larger
than in C & G because they have calculated the rate for a single K
electron.
- The ratio of the decay rate by this process to normal positron
decay is easily calculated because the same nuclear matrix element
appears in both results. We get
where
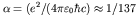 is
the (dimensionless) fine structure constant (Lecture 3) and we neglect
the mass of the neutrino. We can see that for small available energies
this ratio is made large by the smallness of
is
the (dimensionless) fine structure constant (Lecture 3) and we neglect
the mass of the neutrino. We can see that for small available energies
this ratio is made large by the smallness of
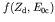 (and is infinite if positron decay is not permitted
energetically); it is also relatively large for high
(and is infinite if positron decay is not permitted
energetically); it is also relatively large for high 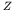 because of
the
because of
the 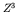 factor.
factor.
- Experiments on electron capture are not as straight-forward as
on normal beta decay. The outgoing neutrino is unobservable. Instead,
what may be detected is an x-ray from transitions in the electron
cloud as the missing K electron is replaced from a higher level,
and/or an Auger electron ejected from the excited electron cloud,
carrying off the energy released as an L-shell electron drops into the
K-shell.
- You have already gone through the (partial) derivation of the
spontaneous emission rate of photons from an excited system (Secs 4.2
and 4.3 in B & J). The final result of this exercise was to derive
the lowest order emission probability per second, or inverse lifetime,
in the dipole approximation,
where 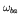 is the angular
frequency corresponding to the energy difference between states
is the angular
frequency corresponding to the energy difference between states 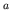 and
and 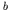 , and
, and
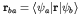 is the
matrix element of the position vector between the wavefunctions of
states
is the
matrix element of the position vector between the wavefunctions of
states 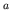 and
and 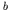 .
.
- The derivation of this result (repeated in somewhat different
form in C & G) is as valid for nuclear photon emission as for
emission from atoms: B & J Eq. [4.71] is identical to C & G
(12.12). The same approximations are valid, particularly the expansion
of the outgoing wave state
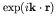 in powers of
in powers of
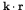 . Clearly since nuclei are much smaller than atoms, the
spatial extent of the wavefunction will be much smaller, resulting in
a much smaller value for
. Clearly since nuclei are much smaller than atoms, the
spatial extent of the wavefunction will be much smaller, resulting in
a much smaller value for
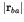 , but this is compensated for
by much larger values of
, but this is compensated for
by much larger values of 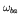 than are found for atoms. In
fact the order of magnitude of the emission rate for allowed nuclear
transitions,
than are found for atoms. In
fact the order of magnitude of the emission rate for allowed nuclear
transitions,
is quite a lot larger than the characteristic rate for allowed
atomic transitions
- Since atoms - in most interesting contexts - collide with one
another and so can de-excite collisionally if radiation is forbidden
(i.e. highly suppressed), they rarely emit much radiation which is not
allowed in the lowest dipole approximation. In contrast, nuclei often
find themselves with no means of de-exciting from an excited state
other than photon radiation. If an excited state differs from all
lower states by several units of angular momentum, radiation will be
possible only by a rather high multipole, and since each higher
multipole of electric radiation is slower at nuclear energies by a
factor of order
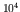 than the next lower multipole, lifetimes of
radiative decay can sometimes be quite long even by human
standards. In this case we speak not of metastable but of isomeric states; such states may be stable enough to make it into the
handbooks....
than the next lower multipole, lifetimes of
radiative decay can sometimes be quite long even by human
standards. In this case we speak not of metastable but of isomeric states; such states may be stable enough to make it into the
handbooks....
- Another (electromagnetic) process which competes with radiation,
especially if it is rather forbidden, is internal conversion. In
this process, the nucleus transfers its excitation energy directly to
an atomic electron (usually a K-shell electron) which is ejected,
carrying off the excitation energy. The matrix elements of the two
processes are similar, but the increasing concentration of the K-shell
electrons near the nucleus as
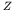 increases means that internal
conversion competes increasingly well with photon emission as
increases means that internal
conversion competes increasingly well with photon emission as 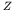 increases. Note that there is no photon involved here; the energy is
transferred directly to the atomic electron.
increases. Note that there is no photon involved here; the energy is
transferred directly to the atomic electron.
Beta and gamma decays
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html lec11-beta_gamma.tex
The translation was initiated by on 2002-04-08


2002-04-08